202. 快乐数

题目

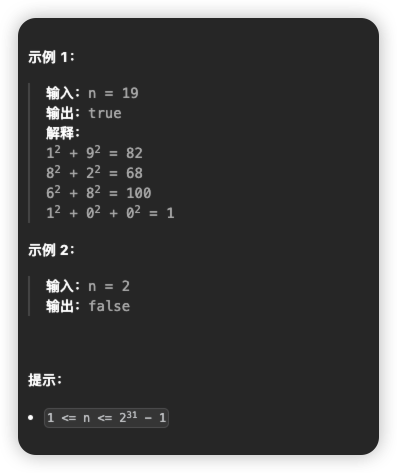
编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

alt text

题解

这道题我们可以转换为判断一个链表是否有环

比如：

如果遍历某个节点为 1，说明链表没环，就是快乐数
如果遍历到重复的节点值，说明有环，就不是快乐数

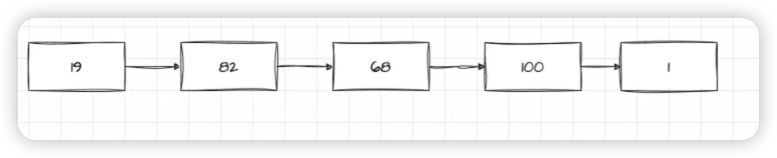
我们用两张图来表示：没环，是快乐数的图：

alt text 有环，不是快乐数的图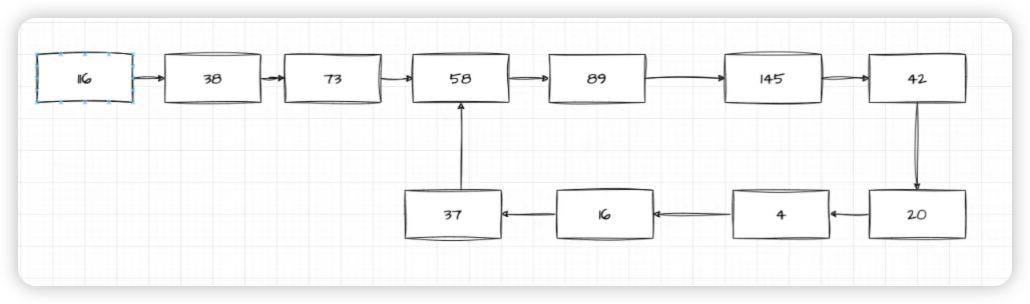：下面我们来实现下代码：

var isHappy = function (n) {
  let pre = n,
    cur = getNext(n)

  while (pre !== cur && cur !== 1) {
    pre = getNext(pre)
    cur = getNext(getNext(cur))
  }

  return cur === 1
}

首先我们需要定义两个快慢指针。pre表示慢指针，每次只走一步。cur表示快指针，每次走两步。这里我们提前让快指针先走一步。getNext表示向后走一步的方法。

我们的循环条件是要满足两个条件：

快慢指针不能相当，如果相等则说明有环，那么就不是快乐数（也就是为什么上面让快指针先走一步）
快指针不能为 1，如果为 1 则说明是快乐数最后返回的时候，只需要判断cur是否为 1 就可以了，如果为 1，则说明是快乐数。如果不为 1，则快慢指针相等的时候退出的循环，则说明是有环的，那就不是快乐数。

那么我们来看下getNext是怎么实现的。

var getNext = function (n) {
  let t = 0
  while (n) {
    t += (n % 10) * (n % 10)
    n = Math.floor(n / 10)
  }
  return t
}

那 n = 19 来举例说明。

t += (n % 10) * (n % 10), (n % 10)。通过n % 10可以找到个位数的值，也就是 9，那么t就是 9 * 9,然后通过n = Math.floor(n / 10)来把个位数去掉，19/10为 1.9， Math.floor(1.9)为 1， n就为 1，进入下一次循环，每次循环的结果t叠加，就可以得到我们希望的值。

完整代码

var isHappy = function (n) {
  let pre = n,
    cur = getNext(n)

  while (pre !== cur && cur !== 1) {
    pre = getNext(pre)
    cur = getNext(getNext(cur))
  }

  return cur === 1
}

var getNext = function (n) {
  let t = 0
  while (n) {
    t += (n % 10) * (n % 10)
    n = Math.floor(n / 10)
  }

  return t
}

202. 快乐数 ​

题目 ​

题解 ​

完整代码 ​

202. 快乐数

题目

题解

完整代码